atlas  0.6
Public Member Functions | Protected Member Functions | Private Member Functions | Private Attributes | List of all members
atlas::weyl::TwistedWeylGroup Class Reference

#include <weyl.h>

Collaboration diagram for atlas::weyl::TwistedWeylGroup:
Collaboration graph
[legend]

Public Member Functions

 TwistedWeylGroup (const WeylGroup &, const Twist &)
 
 TwistedWeylGroup (const TwistedWeylGroup &, tags::DualTag)
 
const WeylGroup & weylGroup () const
 
size_t rank () const
 
int mult (WeylElt &w, Generator s) const
 
void mult (WeylElt &w, const WeylElt &v) const
 
void mult (WeylElt &w, const WeylWord &ww) const
 
int leftMult (WeylElt &w, Generator s) const
 
void leftMult (WeylElt &w, const WeylWord &ww) const
 
WeylWord word (const WeylElt &w) const
 
WeylElt prod (const WeylElt &w, Generator s) const
 
WeylElt prod (Generator s, const WeylElt &w) const
 
WeylElt prod (const WeylElt &w, const WeylElt &v) const
 
WeylElt prod (const WeylElt &w, const WeylWord &ww) const
 
WeylElt prod (const WeylWord &ww, const WeylElt &w) const
 
bool hasDescent (Generator s, const WeylElt &w) const
 
bool hasDescent (const WeylElt &w, Generator s) const
 
Generator twisted (Generator s) const
 
WeylElt twisted (const WeylElt &w) const
 
Generator dual_twisted (Generator s) const
 
WeylElt dual_twisted (const WeylElt &w) const
 
const Twist & twist () const
 
void twist (WeylElt &w) const
 
std::vector< ext_gen > twist_orbits () const
 
Twist dual_twist () const
 
int twistedConjugate (TwistedInvolution &tw, Generator s) const
 
int twistedConjugate (TwistedInvolution &tw, const WeylWord &ww) const
 
int inverseTwistedConjugate (TwistedInvolution &tw, const WeylWord &ww) const
 
TwistedInvolution twistedConjugated (TwistedInvolution tw, Generator s) const
 
void twistedConjugacyClass (TwistedInvolutionList &, const TwistedInvolution &) const
 Puts in c the twistes conjugacy class of w. More...
 
void twistedConjugate (TwistedInvolution &tw, const WeylElt &w) const
 Twisted conjugates element |tw| by |w|: 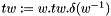$tw:=w.tw.\delta(w^{-1})$. More...
 
bool hasTwistedCommutation (Generator, const TwistedInvolution &) const
 Tells whether |w| twisted-commutes with |s|: $s.w.(s)=w$. More...
 
unsigned long involutionLength (const TwistedInvolution &tw) const
 Returns the length of |tw| as a twisted involution. More...
 
InvolutionWord involution_expr (TwistedInvolution tw) const
 Returns a reduced expression of |tw| as a twisted involution. The second form assures the lexicographically first possible form is used. More...
 
InvolutionWord canonical_involution_expr (TwistedInvolution tw) const
 
InvolutionWord extended_involution_expr (TwistedInvolution tw) const
 
RootNbrList simple_images (const RootSystem &rs, const TwistedInvolution &tw) const
 Roots that are images of the simple roots under involution of |tw|. More...
 
WeightInvolution involution_matrix (const RootSystem &rs, const TwistedInvolution &tw) const
 Matrix of involution of |tw| in adjoint coordinates. More...
 

Protected Member Functions

 TwistedWeylGroup (const TwistedWeylGroup &g)
 

Private Member Functions

void operator= (const TwistedWeylGroup &)
 

Private Attributes

const WeylGroup & W
 
const Twist d_twist
 

Constructor & Destructor Documentation

atlas::weyl::TwistedWeylGroup::TwistedWeylGroup ( const TwistedWeylGroup &  g)
inlineprotected
atlas::weyl::TwistedWeylGroup::TwistedWeylGroup ( const WeylGroup &  d_W,
const Twist &  twist 
)
atlas::weyl::TwistedWeylGroup::TwistedWeylGroup ( const TwistedWeylGroup &  tW,
tags::DualTag   
)

Member Function Documentation

InvolutionWord atlas::weyl::TwistedWeylGroup::canonical_involution_expr ( TwistedInvolution  tw) const
Twist atlas::weyl::TwistedWeylGroup::dual_twist ( ) const
Generator atlas::weyl::TwistedWeylGroup::dual_twisted ( Generator  s) const
inline
WeylElt atlas::weyl::TwistedWeylGroup::dual_twisted ( const WeylElt &  w) const
InvolutionWord atlas::weyl::TwistedWeylGroup::extended_involution_expr ( TwistedInvolution  tw) const
bool atlas::weyl::TwistedWeylGroup::hasDescent ( Generator  s,
const WeylElt &  w 
) const
inline
bool atlas::weyl::TwistedWeylGroup::hasDescent ( const WeylElt &  w,
Generator  s 
) const
inline
bool atlas::weyl::TwistedWeylGroup::hasTwistedCommutation ( Generator  s,
const TwistedInvolution &  tw 
) const

Tells whether |w| twisted-commutes with |s|: $s.w.(s)=w$.

Precondition: |w| is a twisted involution: $w^{-1}=(w)$. Therefore twisted commutation is equivalent to $s.w$ being a twisted involution.

This is in fact the case if and only if $s.w.(s)$ has the same length as $w$, by the following reasoning. Suppose first that $s.w$ is reduced, then its twisted inverse $w.(s)$ is reduced as well. Then the only possible reduction in $s.w.(s)$ is cancellation of the extremal generators; whether this reduction applies is equivalent to having twisted commutation. If $s.w$ is not reduced, then neither is $w.(s)$, and $w'=s.w.(s)$ is a twisted involution not longer than $w$. If it is strictly shorter then obviously twisted commutation fails. In the remaining case that $l(s.w.(s))=l(w)$, let $v=s.w$ so that $w=s.v$ and $w'=v.(s)$ are reduced, but $w.(s)=s.v.(s)$ does reduce, which can only be by cancelling the extremal generators: $s.v.(s)=v$ which implies $w'=w$, and one has twisted commutation.

int atlas::weyl::TwistedWeylGroup::inverseTwistedConjugate ( TwistedInvolution &  tw,
const WeylWord &  ww 
) const
inline
InvolutionWord atlas::weyl::TwistedWeylGroup::involution_expr ( TwistedInvolution  tw) const

Returns a reduced expression of |tw| as a twisted involution. The second form assures the lexicographically first possible form is used.

Precondition: tw is a twisted involution: $tw^{-1}=(tw)$.

The argument given under |hasTwistedCommutation| shows that for every generator |s| exactly one of $s.tw$ and $s.tw.(s)$ is a twisted involution distinct from $tw$, and that if $l(s.tw)<l(tw)$ (for the usual length function on the Weyl group) then the length of this new twisted involution is less than that of $tw$ (by 1 or 2, respectively). A "reduced expression as a twisted involution" for $tw$ is obtained by iterating this to bring the length down to $0$. Working back from the identity (so reading our expression from right to left), it can be determined for each letter to which if the two types of transformation it corresponds; nevertheless, we encode which case prevails in the sign of the generator recorded: we bitwise-complement for the case of conjugation.

Although not immediately obvious, all such reduced expressions do have the same length.

The code below chooses the first possible generator (for the internal numbering, as returned by |leftDescent|) at each step, so the reduced expression found is lexicographically first for the internal renumbering.

WeightInvolution atlas::weyl::TwistedWeylGroup::involution_matrix ( const RootSystem &  rs,
const TwistedInvolution &  tw 
) const

Matrix of involution of |tw| in adjoint coordinates.

unsigned long atlas::weyl::TwistedWeylGroup::involutionLength ( const TwistedInvolution &  tw) const

Returns the length of |tw| as a twisted involution.

Returns the length of tw as a twisted involution.

Precondition: tw is a twisted involution;

Algorithm: this is a simplified version of |involutionOut| that records only the length. This statistic plays a predominant role in the kgb and block structures; avoid calling this in sorting routines, since it is inefficient in such circumstances; instead do with the stored length information there.

int atlas::weyl::TwistedWeylGroup::leftMult ( WeylElt &  w,
Generator  s 
) const
inline
void atlas::weyl::TwistedWeylGroup::leftMult ( WeylElt &  w,
const WeylWord &  ww 
) const
inline
int atlas::weyl::TwistedWeylGroup::mult ( WeylElt &  w,
Generator  s 
) const
inline
void atlas::weyl::TwistedWeylGroup::mult ( WeylElt &  w,
const WeylElt &  v 
) const
inline
void atlas::weyl::TwistedWeylGroup::mult ( WeylElt &  w,
const WeylWord &  ww 
) const
inline
void atlas::weyl::TwistedWeylGroup::operator= ( const TwistedWeylGroup &  )
private
WeylElt atlas::weyl::TwistedWeylGroup::prod ( const WeylElt &  w,
Generator  s 
) const
inline
WeylElt atlas::weyl::TwistedWeylGroup::prod ( Generator  s,
const WeylElt &  w 
) const
inline
WeylElt atlas::weyl::TwistedWeylGroup::prod ( const WeylElt &  w,
const WeylElt &  v 
) const
inline
WeylElt atlas::weyl::TwistedWeylGroup::prod ( const WeylElt &  w,
const WeylWord &  ww 
) const
inline
WeylElt atlas::weyl::TwistedWeylGroup::prod ( const WeylWord &  ww,
const WeylElt &  w 
) const
inline
size_t atlas::weyl::TwistedWeylGroup::rank ( ) const
inline
RootNbrList atlas::weyl::TwistedWeylGroup::simple_images ( const RootSystem &  rs,
const TwistedInvolution &  tw 
) const

Roots that are images of the simple roots under involution of |tw|.

const Twist& atlas::weyl::TwistedWeylGroup::twist ( ) const
inline
void atlas::weyl::TwistedWeylGroup::twist ( WeylElt &  w) const
inline
std::vector< ext_gen > atlas::weyl::TwistedWeylGroup::twist_orbits ( ) const
Generator atlas::weyl::TwistedWeylGroup::twisted ( Generator  s) const
inline
WeylElt atlas::weyl::TwistedWeylGroup::twisted ( const WeylElt &  w) const
inline
void atlas::weyl::TwistedWeylGroup::twistedConjugacyClass ( TwistedInvolutionList &  c,
const TwistedInvolution &  tw 
) const

Puts in c the twistes conjugacy class of w.

Algorithm: straightforward enumeration of the connected component of |w| in the graph defined by the operation twistedConjugate, using a |std::set| structure to record previously encountered elements and a |stdstack| to store elements whose neighbors have not yet been generated.

int atlas::weyl::TwistedWeylGroup::twistedConjugate ( TwistedInvolution &  tw,
Generator  s 
) const
inline

$. For consistency, these functions should have |s| resp. |ww| as first argument

int atlas::weyl::TwistedWeylGroup::twistedConjugate ( TwistedInvolution &  tw,
const WeylWord &  ww 
) const
inline
void atlas::weyl::TwistedWeylGroup::twistedConjugate ( TwistedInvolution &  tw,
const WeylElt &  w 
) const

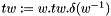Twisted conjugates element |tw| by |w|: $tw:=w.tw.\delta(w^{-1})$.

TwistedInvolution atlas::weyl::TwistedWeylGroup::twistedConjugated ( TwistedInvolution  tw,
Generator  s 
) const
inline
const WeylGroup& atlas::weyl::TwistedWeylGroup::weylGroup ( ) const
inline
WeylWord atlas::weyl::TwistedWeylGroup::word ( const WeylElt &  w) const
inline

Member Data Documentation

const Twist atlas::weyl::TwistedWeylGroup::d_twist
private
const WeylGroup& atlas::weyl::TwistedWeylGroup::W
private
The documentation for this class was generated from the following files:
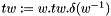Generated by   doxygen 1.8.11